We want to talk about a project based on the work of u/DaVinci103. Since its inception, the bruijn programming language had support for positive and negative integers. One thing I love about lambda calculus encodings for numbers is that they are usually infinitely precise – only limited by your computer’s memory. Still, lazy (call-by-need) or optimal reducers can sometimes do magical optimizations automatically that would have to be hard-coded in other languages. It’s natural to want to extend the integers to arbitrary-precision fractions, and later real and complex numbers. Encoding rational numbers, it turns out, is as easy as writing two integers as a (Church) pair. The relevant arithmetic operations are fairly trivial to implement as well. However, for the real numbers, I couldn’t come up with any elegant solution: This is, until I saw a great post on Reddit about this exact topic. So, in this article, I want to show how the new arbitrary-precision arithmetic of bruijn is implemented, including some “more mathematical” real/complex formulas and ways to approximate their result. I also want to use this opportunity to introduce you to coding in bruijn and lambda calculus in general. Note that all of the definitions (including library imports) have a 1:1 correspondence to pure lambda calculus – bruijn is just syntactic sugar (syntax explanation). We’re literally crafting complex formulas from the bottom up. You can click on any identifier to jump to its definition.
 Integer
Integer
Natural numbers in lambda calculus are most commonly encoded as Church numerals. They can be extended to integers by writing them as a pair. While the implementations are quite small and elegant, any number now takes O(2^n) space. Instead, I use balanced ternary numbers. Theoretically, one could use any base, but an investigation by Torben Mogensen showed that bigger bases result in much more complicated implementations without significant performance benefits.
Balanced ternary numbers provide a very elegant way to denote negative numbers by assigning one of its three digits to a negative multiplier. This encoding reduces the space needed to O(log n).
 Rational
Rational
The rational numbers represent the ratio between two integers. The obvious implementation is to use a pair of two balanced ternary numbers. Since we have the restriction of a non-zero denominator, we subtract 1 from the denominator in the encoding.
Operators for rational numbers can be implemented by comparing the product of the numerators and denominators. Basic operations like addition, subtraction, multiplication, and division can be implemented similarly.
 Real
Real
The missing insight I got from Reddit is a lambda calculus translation of the fact that real numbers can be defined as the infinite limit of a function that maps natural to rational numbers. For example, for some x ∈ R, there exists f_x: N → Q, such that x = lim_{n→∞} f_x(n). This would typically be defined as a sequence that converges to the desired real number.
Approximating a real number to an arbitrarily precise rational number can then be done by applying some natural number. In theory, we could use any base here, yet I still use balanced ternary.
 Operators
Operators
To check equality of two real numbers, we compare the infinite limits of their respective sequences. For other binary operators, a small combinator trick "joins" the argument of both sides, such that we only ever need to apply a single number to any real number to get its approximation.

 Power
Power
For positive numbers, the power function can be implemented using the exponential and logarithmic functions. The exponential function can be approximated using Taylor series, while the logarithmic function can be approximated using a series expansion.
 Derivation
Derivation
The derivative of a function can be approximated using the limit definition of the derivative. This involves calculating the difference quotient and taking the limit as the increment approaches zero.
 Constants
Constants
Interesting constants like e and π can be calculated using series expansions. For example, e can be calculated using the Taylor series of the exponential function, and π can be approximated using a series expansion.
 Trigonometry
Trigonometry
Trigonometric functions like arctan, sin, and cos can be approximated using series expansions. These functions are left as an exercise to the reader.
 Methods
Methods
There are many ways to translate real approximations like Taylor series to lambda calculus. Depending on your needs, different methods may be more optimal.
 Unary
Unary
If you use unary/Church numerals instead, you get repeated iteration for free. A Church numeral is essentially a repeated application of a function. This can make certain calculations easier but also takes more space.

 Recurrence
Recurrence
Recurrence relations can be resolved using a variadic fixed-point combinator. However, this doesn't necessarily give performance improvements over normal iteration using y-recursion.
 Complex
Complex
Complex numbers are just a pair of real numbers. The approximation arguments of the two real numbers are lifted to the outside, such that we only ever need to apply a single natural number. Operators for complex numbers can be implemented using rational operations directly.
 Lessons
Lessons
Working with bruijn and pure lambda calculus is satisfying and enjoyable, but it comes with performance disadvantages. If someone wanted to use this for actual programs, they would need to invest a huge amount of work to make all of these functions efficient and accurate. This article serves mostly as a fun proof of concept and notebook.
Remember these 3 key ideas for your startup:
- Efficiency in Encoding: Using balanced ternary numbers instead of larger bases can significantly improve the efficiency of your algorithms. This can be crucial for startups looking to optimize their computational resources.
- Lambda Calculus for Precision: Lambda calculus allows for infinitely precise calculations, limited only by your computer's memory. This can be a game-changer for startups dealing with high-precision computations.
- Iterative Improvements: The article demonstrates the importance of iterative improvements and optimizations. For startups, this means continuously refining your algorithms and processes to achieve better performance and accuracy.
Edworking is the best and smartest decision for SMEs and startups to be more productive. Edworking is a FREE superapp of productivity that includes all you need for work powered by AI in the same superapp, connecting Task Management, Docs, Chat, Videocall, and File Management. Save money today by not paying for Slack, Trello, Dropbox, Zoom, and Notion.
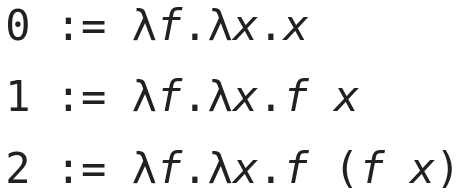
For more details, see the original source.






